107. 二叉树的层次遍历 II
题目描述
给定一个二叉树,返回其按层次遍历的节点值。 (即逐层地,从左到右访问所有节点)。
例如:
给定二叉树: [3,9,20,null,null,15,7],
返回其自底向上的层次遍历为::[[15,7],[9,20],[3]]
解答
思考
解答了102题,这一题,就相对而言比较简单了。
也就是将前面的插入的位置做一个变化,不使用append,而直接插入到列表的首位即可。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def levelOrderBottom(self, root: TreeNode) -> List[List[int]]:
if root is None:
return []
result = []
que = [[root, 0]]
while len(que) > 0:
node = que.pop(0)
root = node[0]
level = node[1]
if len(result) == level:
result.insert(0,[])
result[0].append(root.val)
if root.left is not None:
que.append([root.left, level+1])
if root.right is not None:
que.append([root.right, level+1])
return result结果: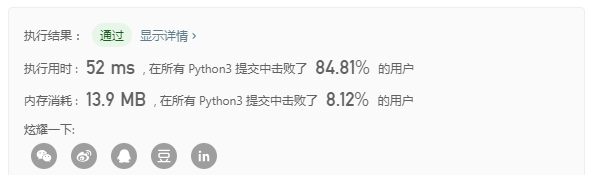
方法二
和上面的思想一样,不过修改102的第一种解法。
殊途同归。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def levelOrderBottom(self, root: TreeNode) -> List[List[int]]:
if root is None:
return []
result = []
que = [root]
while len(que) > 0:
size = len(que)
temp_list = []
while size > 0:
root = que.pop(0)
temp_list.append(root.val)
if root.left is not None:
que.append(root.left)
if root.right is not None:
que.append(root.right)
size = size - 1
result.insert(0, temp_list)
return result结果: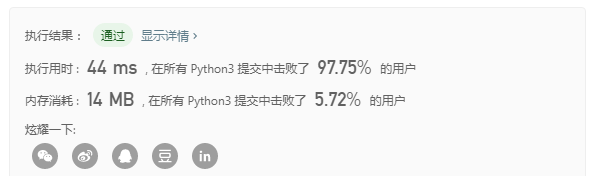
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/binary-tree-level-order-traversal-ii/




