leetcode-70 | 爬楼梯

70. 爬楼梯

题目描述

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
注意：给定 n 是一个正整数。

示例 1：
输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。

1. 1 阶 + 1 阶
2. 2 阶

示例 2：
输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。

1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

思路

动态规划

原文地址。先来张图：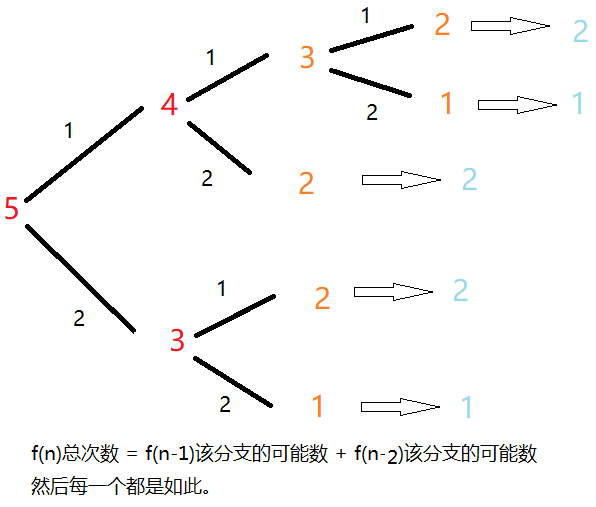

也就是总体可以是由每一个重复的单元构成的。
观察也不难看出这个情况类似于斐波拉契数列，下面就来代码实现：

class Solution:
    def climbStairs(self, n: int) -> int:
        if n == 1:
            return 1
        elif n == 2:
            return 2
        else:
            return self.climbStairs(n-1) + self.climbStairs(n-2)     

由于是递归的原因，这里超时了。

改进

也就是根据这个数列的特性，只需要两个指针来保存数据值。如下图：

class Solution:
    def climbStairs(self, n: int) -> int:
        # f(n) = f(n-1) + f(n-2)
        # f(1) = 1, f(2) = 2 , f(3) = 3, f(4)=5, f(5)=8
        a = b = 1
        for i in range(1, n):
            temp = b
            b = a + b
            a = temp
        return b

结果：

---

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/climbing-stairs