leetcode-69 | x的平方根

题目描述

实现 int sqrt(int x) 函数。
计算并返回 x 的平方根，其中x 是非负整数。
由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

示例 1:
输入: 4
输出: 2

示例 2:
输入: 8
输出: 2
说明: 8 的平方根是 2.82842…,
由于返回类型是整数，小数部分将被舍去。

思路解答

暴力解决问题

暴力解决，遍历一遍[1,x]，然后计算i*i==x?，当然由于是整除，故而需要记录前一个位置的i值，当i*i>x时，返回i-1。
当然，这种方法不可取。会超时。

二分法

很巧妙，网上别个用了二分法，就把数据从O(n)级别降到了O(log2(n))级别。具体的实现如下：

class Solution:
    def mySqrt(self, x: int) -> int:
        if x == 0 or x == 1:
            return x
        left = 1
        right = x
        mid = (1 + x) // 2
        while left <= right:
            if mid == x // mid:  # 整除，而不是乘
                return mid
            elif mid > x // mid:
                right = mid - 1
            else:
                left = mid + 1
            mid = (left + right) // 2
        return mid

至于为什么用整除，而不是用乘法运算，其实也不难理解，这里用两个案例说话：
5 sqrt => 2 而 2 * 2 = 4，还需要进一步判断(2*2<5 && 3*3>5)才能确定是2
2 = 5 // 2 完美成立。
故而用整除还是比较完美。

结果：

牛顿迭代法

我这里给出原文博客链接，下面我弄成了图片的，方便理解：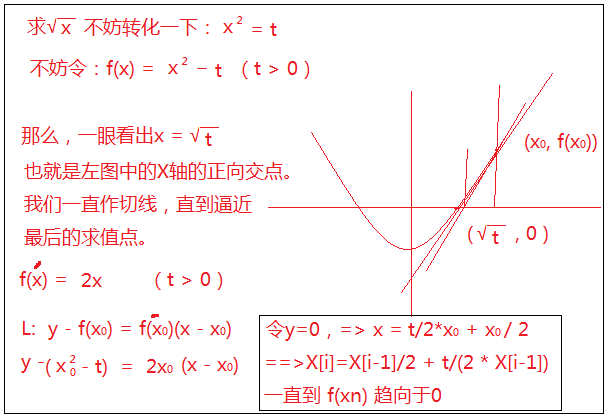

思路很清晰，这里不妨就来实现：

class Solution:
    def mySqrt(self, x: int) -> int:
        # 取x0 = x
        # X[i]=X[i-1]/2 + t/(2 * X[i-1])
        x0 = t = x
        while abs(x0*x0 - t) > 0.000001:
            x0 = x0 / 2 + t / (2 * x0)
        return int(x0)

结果：

---

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/sqrtx