动态规划
找最短路径问题
求A->G的最短代价路径。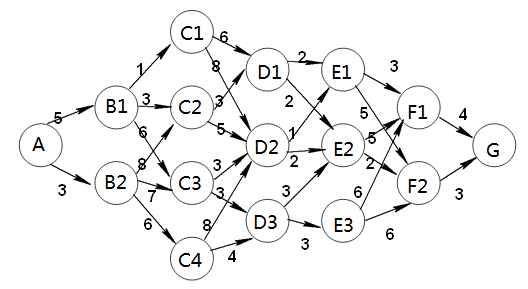
简单举个例子,从A到B,我们选择不同的路径,就会有不同的代价。这个选择过程叫做决策。
这整个问题是一个前后关联具有链状结构的多阶段过程,称为多决策过程。
在多决策问题中,各个阶段所采取的决策,依赖于当前状态。一个决策序列就是在变化的状态中产生出来的。
将这种解决多阶段决策最优化的过程称之为动态规划。
动态规划VS分治
分治算法:将问题划分成互不相交的子问题,递归的求解子问题,然后将他们的解组合起来,以求出原问题的解。
动态规划:从上面的图片不难看出,前一阶段的终点是后一阶段的起点,前一阶段的决策变量是后一阶段的状态变量。也就是动态规划应用于子问题重叠的情况,即不同的子问题具有公共的子子问题。子问题的求解是递归,将其划分成更小的子子问题。
动态规划一般用来求解最优解的问题。动态规划的最优化概念是在一定条件下,找到一种途径,在各个阶段的效益经过按问题具体性质所确定的运算以后,使得全过程的总效益达到最优。
动态规划重要特性
如果说A->B->C->D是A到D最短路线,那么从A到C的最短路线一定是A->B->C。
也就是说我们可以从终点逐段向始点方向寻找最短路线。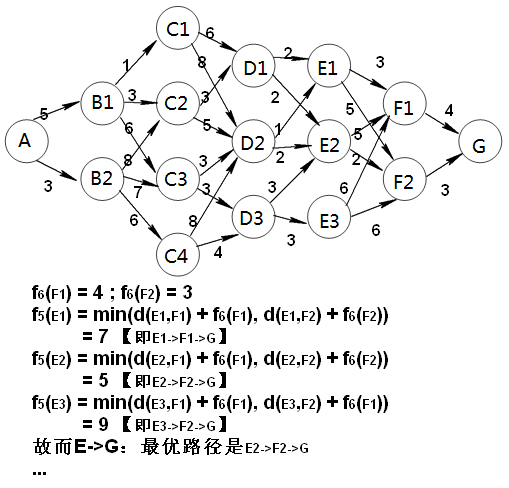
计算的时候是计算如:f(A,G) = min{d(A, B1) + f(B1, G), d(A, B2) + f(B2, G)}
的式子,显然f(G, G) = 0, f(F1, G) = 4, f(F2, G) = 3
不难看出这里最后的计算是从后往前计算,也就是所谓的逆推解法。
逆推求解
下面就来讲上面的A->G的最短代价路径问题逆推求解。
我们用邻接表结构来存储数据,为了方便对状态表示,我们这里就将A-G编码。
状态AB1B2C1C2C3C4 D1D2D3E1E2E3F1F2G
编码0123456 789101112131415
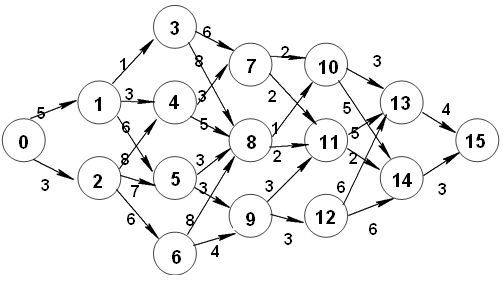
首先生成邻接表表示
#include
using namespace std;
typedef struct Node{
int index; //节点的下标
int value; // 节点的值
struct Node * next; //指向下一个节点的指针
}Node;
struct ev{
int value1, value2, weight;
}; // 边类型
ev values[] = {
{0,1,5},{0,2,3},
{1,3,1},{1,4,3},
{1,5,6},{2,4,8},
{2,5,7},{2,6,6},
{3,7,6},{3,8,8},
{4,8,5},{4,7,3},{5,8,3},{5,9,3},{6,8,8},
{6,9,4},{7,10,2},{7,11,2},{8,10,1},{8,11,2},{9,11,3},{9,12,3},
{10,13,3},{10,14,5},{11,13,5},{11,14,2},{12,13,6},{12,14,6},{13,15,4},
{14,15,3}
};
//打印所有节点
void testData(Node list[16]){
Node *p = NULL;
int count = 0;
for(int i=0; i<16; i++){
p = list[i].next;
while(p){
count += 1;
cout<<"("<index<<","<value<<")";
p = p->next;
}
}
cout<<"\n一共"<index = nextNode;
s->value = weight;
//指针连接
s->next = plist[preNode]->next;
plist[preNode]->next = s;
}
//测试一下
testData(list);
return 0;
}
测试结果截图: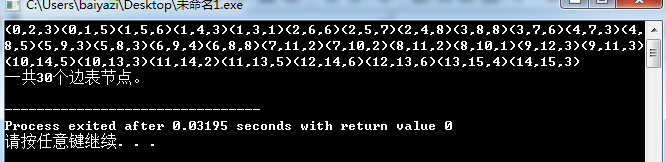
然后计算最小代价路径
接下来就是操作这个数据,求出最小的代价路径。
#include
using namespace std;
typedef struct Node{
int index; //节点的下标
int value; // 节点的值
struct Node * next; //指向下一个节点的指针
}Node;
struct ev{
int value1, value2, weight;
}; // 边类型
ev values[] = {
{0,1,5},{0,2,3},
{1,3,1},{1,4,3},
{1,5,6},{2,4,8},
{2,5,7},{2,6,6},
{3,7,6},{3,8,8},
{4,8,5},{4,7,3},{5,8,3},{5,9,3},{6,8,8},
{6,9,4},{7,10,2},{7,11,2},{8,10,1},{8,11,2},{9,11,3},{9,12,3},
{10,13,3},{10,14,5},{11,13,5},{11,14,2},{12,13,6},{12,14,6},{13,15,4},
{14,15,3}
};
void testData(Node list[16]){
Node *p = NULL;
int count = 0;
for(int i=0; i<16; i++){
p = list[i].next;
while(p){
count += 1;
cout<<"("<index<<","<value<<")";
p = p->next;
}
}
cout<<"\n一共"<index = nextNode;
s->value = weight;
//指针连接
s->next = plist[preNode]->next;
plist[preNode]->next = s;
}
// testData(list);
//下面就是动态规划求最小代价的路径问题
// f(0,15) = min(d(0,1) + f(1, 15) + d(0, 2) + f(2, 15))
// 由于f(x, 15),后面的都是15,故而用数组表示即可
int F[16], x[16];
for(int i=0;i<16;i++){
F[i] = 999;
}
F[15] = 0;
for(int i=14; i>=0; i--){
Node* p = plist[i]->next;
// 求i这个节点到G点的最小代价值,得到的结果存入F[i]
int min_val = 999;
// 求i这个节点在最小代价的时候,的下一个节点是哪个?,记录到数组x中x[i]
int min_index = p->index;
while(p){
int nextNode = p->index;
int weight = p->value;
if(weight + F[nextNode] < min_val){
min_val = weight + F[nextNode];
min_index = nextNode;
}
p = p->next;
}
F[i] = min_val;
x[i] = min_index;
}
int i = 0;
cout<<"路径是:"<<i;
while(i<15){
cout<<" "<<x[i];
i = x[i];
}
cout<<"\n总代价是:"<<F[0]<<endl;
return 0;
}
结果: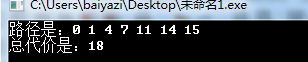
这里比较难理解的是关于代价路径。
提示一下,因为我们每一次在跟新F[i]的时候,就记录了该节点到G的最优的下一个节点是x[i]。
但是,在A->G的路径中不是所有的节点都用到的,也就是如13号节点,它到G点,毫无疑问在本轮中得出最小的代价为4,此时记录该节点的下一个节点(即15,将15存入x[13])和代价值4。但是在计算11号节点的时候,遍历所有边表,找到最小代价节点是14,记录14,即x[11] = 14,F[11]=5。
同理,计算下面的节点的最小代价路径上的下一个节点:
x[11] = 14,x[14] = 15 , x[13] = 15, x[12] = 14
故而从11号节点到15号节点是:11->14->15
可以从我们上面记录的x数组得出:11->x[11]->x[x[11]]
而12和13节点这里就多余了。




