分而治之(divide-and-conquer)

分而治之(divide-and-conquer)

简单了解

算法分析与设计：

1. 分治法的设计思想：
   将一个难以直接解决的大问题，分割成一些规模比较小的相同问题，以便各个击破，分而治之。
2. 分治策略是：
   对于一个规模为n的问题，若该问题可以容易地解决（比如说规模n比较小则直接解决，否则将其分解为k个规模较小的子问题，这些子问题相互独立且与原问题形式相同，递归地解决这些子问题，然后将各个子问题的解合并得到原问题的解。
3. 分治法所能解决的问题一般具有以下几个特征：
   ①该问题的规模缩小到一定的程度就可以容易地解决；
   ②该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质；【能用分治法解决问题的前提】
   ③利用该问题分解出的子问题的解可以合并为该问题的解；【能用分治法解决问题的关键】
   ④该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子子问题。
   具备了第一条和第二条特征，而且不具备第三条特征，考虑使用贪心法或动态规划。
   具备了第一条、第二条特征和第三特征，而不具备第四条特征，一般考虑动态规划。
4. 三个步骤
   ①分解：将原问题分解成为若干个规模较小、相互独立、与原问题形式相同的子问题；
   ②解决：若子问题的规模较小而容易被直接解决则直接解，否则递归地解各个子问题；
   ③合并：将各个子问题的解合并为原问题的解。

算法基础（第五版）：
将一个问题的实例划分为两个或者更多个较小的实例。这些较小的实例通常也是原问题的实例。如果可以轻松获取小问题实例的答案，那么通过合并这些答案，就能得出原实例的答案。如果这些较小的实例还是太大，难以轻松解决，可以将它们划分为再小一些的实例。一直持续这一实例划分过程，直到其规模小的可以轻松获取得到答案为止。

分而治之是一种自顶向下(top-down)的方法。
通过向下获得较小的实例的答案，以获得一个问题的答案。不难发现递归就是使用这种方法。

从案例开始

二分法查找的递归案例，给定数列[5,12,23,36,39,50,62,73,80,99]，查找23。

class Solution:
    def __init__(self, list, x):
        self.list = list
        self.x = x
    def divide(self, low, high):
        if len(self.list) == 0 or low > high:
            return 0
        mid = (low + high) // 2
        if self.x == self.list[mid]:
            return mid
        elif self.x > self.list[mid]:
            return self.divide(mid + 1, high)
        else:
            return self.divide(low, mid - 1)

if __name__ == '__main__':
    a = [5,12,23,36,39,50,62,73,80,99]
    print(Solution(a, 23).divide(0, len(a)-1))

这个案例中我遇到的问题：关于if-else分支中的return
顺这思路写代码的过程中，我就写成了这样：

if self.x == self.list[mid]:
    return mid
elif self.x > self.list[mid]:
    self.divide(mid + 1, high)
else:
    self.divide(low, mid - 1)

而主观的认为在分支if中我已经清晰的表达了我所需要的意思，也就是我那里是可以返回最终的mid的。
但是，却忘记了函数的自调用，也是函数的调用，而返回值是返回在函数的额调用处。
也就是最终的结果是在elif分支中得到值，但是我并没有接收，也没有返回。
故而需要加上return

LeetCode 53题

最大子段和问题：
输入:[-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

思路

（1）划分：按照平衡子问题的原则，将序列(a1, a2, a3, ... , an)划分成长度相同的两个子序列(a1, a2, a3, ... , a(n/2))和(a(n/2)+1, ... , an)，则会出现下面三种情况：
①a1, a2, a3, ... , an的最大子段和 = a1, a2, a3, ... , a(n/2)的最大字段和；
②a1, a2, a3, ... , an的最大子段和 = a(n/2)+1, ... , an 的最大字段和；
③a1, a2, a3, ... , an的最大子段和 = ai+a(i+1)+ ... + a(j-1)+a(j)，[1≤i≤n/2， n/2+1≤j≤n]的最大字段和；
（2）求解子问题：情况①和②递归求解，情况③分别计算：
s1=max(ai+a(i+1)+ ... + n/2) ， 1≤i≤n/2
s2=max(a(n/2+1)+ ... + an) ，n/2+1≤j≤n
也就是说必含有两端断口的序列项。
（3）合并：取三者之中较大者为原问题的解。

代码实现

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        n = len(nums)
        #序列长度为1，直接计算
        if n == 1:
            return nums[0]
        else:
            #递归计算左半边最大子序和
            max_left = self.maxSubArray(nums[0:len(nums) // 2])
            #递归计算右半边最大子序和
            max_right = self.maxSubArray(nums[len(nums) // 2:len(nums)])
            # 对应情况三
            #计算中间的最大子序和，从右到左计算左边的最大子序和，从左到右计算右边的最大子序和，再相加
            max_l = nums[len(nums) // 2 - 1]
            tmp = 0
            for i in range(len(nums) // 2 - 1, -1, -1):
                tmp += nums[i]
                max_l = max(tmp, max_l)
            max_r = nums[len(nums) // 2]
            tmp = 0
            for i in range(len(nums) // 2, len(nums)):
                tmp += nums[i]
                max_r = max(tmp, max_r)
        #返回三个中的最大值
        return max(max_right,max_left,max_l+max_r)

结果：

这里需要注意的是，递归的效率本来就不高，如果不截取列表，而直接传入原列表到调用，并定义left和right的下表指向，会超时。
在leetcode中，我测试了一下，参数用的列表,left下表,right下表，最后两个没通过，超时。

两路合并(Two-Way-Merging)

和上一题的思路类似，过程如下：
①划分：将数组划分成两个各自包含n/2个数据项的子数组
②求解子问题：解决每个子数组，对其排序。除非数组足够小，否则以递推的方式完成此任务。
③合并：将子数组合并为单个有序数组，以合并这些子数组的答案。

案例

待排序数组：[27,10,12,20,25,13,15,22]，过程分析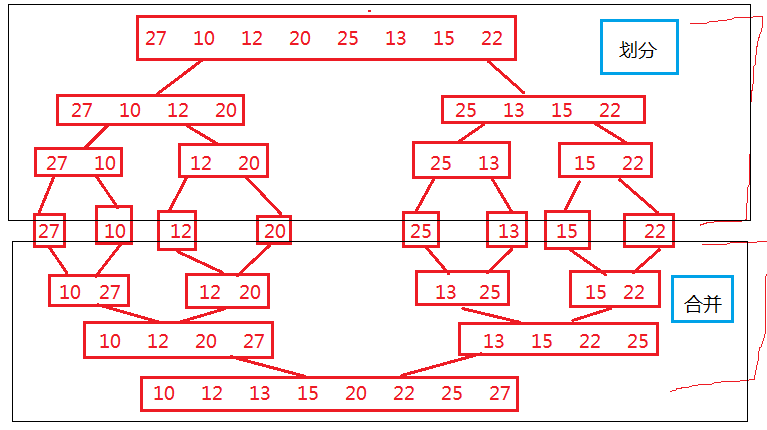

class Solution(object):
    def TwoWayMerging(self, nums):
        print("nums into:" , nums)
        a = nums.copy()
        # 小规模问题，直接求解
        if len(a) == 1 or len(a) == 0:
            return a
        else:
            mid = len(a) // 2
            u = a[:mid]
            v = a[mid:]
            print("U:" , u)
            self.TwoWayMerging(u)
            print("V:" , v)
            self.TwoWayMerging(v)
            # 情况三
            i = j = k = 0
            while i < len(u) and j < len(v):
                # print("k is :" , k)
                if u[i] < v[j]:
                    nums[k] = u[i]
                    i = i + 1
                else:
                    nums[k] = v[j]
                    j = j + 1
                k = k + 1
            while i < len(u):
                nums[k] = u[i]
                i = i + 1
                k = k + 1
            while j < len(v):
                nums[k] = v[j]
                j = j + 1
                k = k + 1
            print("nums out:" , nums)
        return nums

if __name__ == '__main__':
    print(Solution().TwoWayMerging([27,10,12,20,25,13,15,22]) )
    a  = [-8, 5, 10, 12, 13, 15, 20, 22, 25, 27, 33, 200]
    def test(a):
        a[0] = 100
    test(a)
    print(a)

观察前面两个案例的代码，不难发现共同点，第三步的合并，其实也是作用在小规模中的，只是在处理的时候，我们就看做是两个整体列表的排序。
为了观察效果，不妨把案例代码中的print前面的注释去除掉。
然后自己画一个栈，自己模拟一下代码是如何运行的。
比如[14,5,6,23]进入，
u1=[14,5], v1=[6,23]
然后u1作为下一次的nums，进入
u2=[14]，v2=[5]
满足退出条件，然后将v2，u2进行排序，排序完成，记录到nums中，也就是u1，
此时u1=[5,14]。
同理v1，入栈，进入进行相同的操作，得到v1=[6,23]
此时完成了对u1,v1的两部分的排序，然后进行这两个的整体排序，记录到初始传入的列表[14,5,6,23]中。
最后饭后的也是这个列表的排序结果，即：[5,6,14,23]

练习

分治法求一个数组中最大的元素的位置。

class Solution(object):
    def __init__(self, nums):
        self.nums = nums

    def FindMaxPos(self,low, high):
        # 小规模直接得结果
        if low == high:
            return low
        else:
            mid = (low+high) // 2
            left_index = self.FindMaxPos(low, mid)
            right_index = self.FindMaxPos(mid+1, high)
            if self.nums[left_index] < self.nums[right_index]:
                return right_index
            else:
                return left_index

if __name__ == '__main__':
    a = [27,10,12,20,205,13,15,22]
    print(Solution(a).FindMaxPos(0, len(a)-1))   # 4

上面的案例比较简单，不妨看看LeetCode中的分治题目。
leetcode 23题