leetcode-447 | 回旋镖的数量

题目描述

给定平面上 n 对不同的点，“回旋镖” 是由点表示的元组 (i, j, k) ，其中 i 和 j 之间的距离和 i 和 k 之间的距离相等（需要考虑元组的顺序）。
找到所有回旋镖的数量。你可以假设 n 最大为 500，所有点的坐标在闭区间 [-10000, 10000] 中。

示例:
输入:
[[0,0],[1,0],[2,0]]
输出:
2
解释：
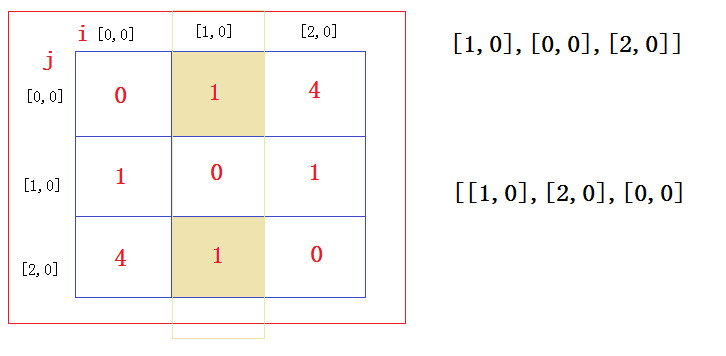
两个回旋镖为 [[1,0],[0,0],[2,0]] 和 [[1,0],[2,0],[0,0]]

解答思路

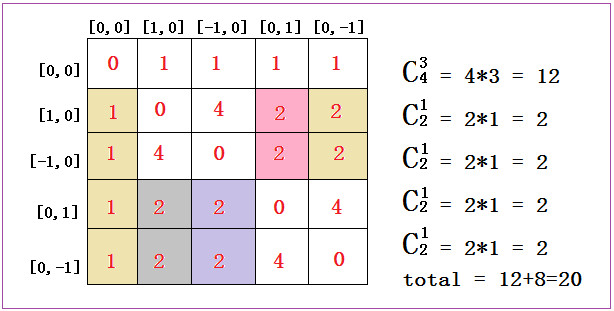
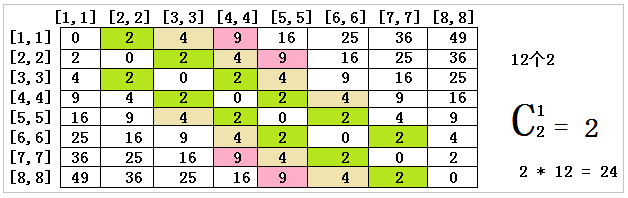
以i为轴，然后计算所有点到i的距离，相等的（即距离相同个数大于2的）就是满足条件的。

我们画个图分析一下：

增加一点数据：

不妨再来一个图解：

因为数据和位置相关，所以这里是取排列。
根据上面的图示分析，我们可以用列表中存列表来存放二维数组，由于我们是按照列或者行来计算的（对称矩阵），所以我们这里的列表的统计方式也要按照列或者行。

翻译如下：

class Solution(object):
    def getD(self, p1, p2):
        return (p1[0]-p2[0])*(p1[0]-p2[0]) + (p1[1]-p2[1]) * (p1[1]-p2[1])

    def numberOfBoomerangs(self, points):
        """
        :type points: List[List[int]]
        :rtype: int
        """
        i = 0
        li = []
        while i < len(points):
            j = 0
            li.append([])
            while j < len(points):
                d = self.getD(points[i], points[j])
                li[i].append(d)
                j+=1
            i+=1

        count = 0
        #统计每一个列表中大于等于2的数据
        for i in li:
            se = set(i)
            for k in se:
                s = i.count(k)
                if s >= 2:
                    count += s * (s-1)

        return count

结果：
超出时间限制
分析：
其实也不难理解，在我们处理统计数据的时候，s = i.count(k)也是O(n)级别。
所以我们算法的时间复杂度是O(n^3)级别，而一般而言在leetcode中，不超时的时间复杂度是O(n^2)。
所以我们需要改进算法。

---

class Solution(object):
    def getD(self, p1, p2):
        return (p1[0]-p2[0])*(p1[0]-p2[0]) + (p1[1]-p2[1]) * (p1[1]-p2[1])

    def numberOfBoomerangs(self, points):
        """
        :type points: List[List[int]]
        :rtype: int
        """
        i = 0
        li = []
        while i < len(points):
            j = 0
            li.append([])
            while j < len(points):
                d = self.getD(points[i], points[j])
                li[i].append(d)
                j+=1
            i+=1


        count = 0
        #统计每一个列表中大于等于2的数据
        for i in li:
            #按照每一个列表（即列），统计数据到字典中
            se = {}
            for k in i:
                se[k] = se.get(k,0) + 1

            #计算
            for m in se.values():
                if m>=2:
                    count += m*(m-1)

            se = {}  #规整为{}


        return count

分析：
时间复杂度是：O(n^2)，满足题意要求。

结果：

执行用时 : 1684 ms, 在Number of Boomerangs的Python3提交中击败了62.50% 的用户
内存消耗 : 23 MB, 在Number of Boomerangs的Python3提交中击败了13.46% 的用户

提交时间	状态	执行用时	内存消耗	语言
几秒前	通过	1684 ms	23MB	python